SNE

SNE 是通过仿射变换将数据点映射到概率分布上，主要包括两个步骤：

SNE构建一个高维对象之间的概率分布，使得相似的对象有更高的概率被选择，而不相似的对象有较低的概率被选择。
SNE在低维空间里构建这些点的概率分布，使得这两个概率分布之间尽可能地相似。

可以看到t-SNE是非监督地降维，它跟kmeans等不同，他不能通过训练得到一些东西之后再用于其他数据（t-SNE只有fit_transform，没有fit操作）

SNE原理推导

SNE是将欧几里得距离转换为条件概率来表达点与点之间地相似度。具体来说，给定一个N个高维地数据点，t-SNE首先是计算概率$p_{ij}$，正比于$x_i$和$x_j$(这种概率是自主构建的)，即：

$p_{j|i}=\frac{exp(-||x_i-x_j||^2/(2\sigma_i^2))}{\sum_{k≠i}exp(-||x_i-x_k||^2/(2\sigma_i^2))}$

这里的有一个参数$\sigma_i$,对于不同的点$x_i$取值不一样，后续会讨论如何设置。此外设置$p_{x|x}=0$，因为我们关注的是两两之间的相似度。那对于低维度下的$y_i$，我们可以指定高斯分布为方差$\frac{1}{\sqrt{2}}$,因此他们之间的相似度如下

$q_{j|i}=\frac{exp(-||y_i-y_j||^2)}{\sum_{k≠i}exp(-||y_i-y_k||^2)}$

同样$q_{i|i}$=0
如果降维效果好，局部特征保留完整，那么$p_{i|j}=q_{i|j}$优化两个分布之间的距离很容易想到KL散度，那么目标函数有：

$C=\sum_iKL(P_i||Q_i)=\sum_i\sum_jp_{j|i}log\frac{p_{j|i}}{q_{j|i}}$

这里$P_i$表示了给定$x_i$下，其他所有数据点的条件概率分布。需要注意的是KL散度具有不对称性，在低维映射不同的距离对应不同的惩罚权重是不同的，具体来说：距离较远的两个点来表达距离较近的两个点会产生更大的cost，相反，用较近的两个点来表达较远的两个点产生的cost相对较小。即用较小的$q_{j|i}$=0.2来建模较大的$p_{j|i}$=0.8,$cost=plog(\frac{p}{q})=1.11$,同样用较大的$q_{j|i}=0.8$来建模较大的$p_{j|i}=0.2$,cost=-0.277，因此SNE倾向于保留数据中的局部特征。

下面开始正式推导SNE:

首先要注意不同的点具有不同的$\sigma_i$,熵$P_i$会随着$\sigma_i$增加而增加
SNE引入了困惑度（perplexity）的概念，用二分搜索方法寻找一个最佳的$\sigma$.其中困惑度表示为

$perp(P_i)=2^{H(P_i)}$

这里$H(P_i)是P_i的熵$,即：

$H(P_i)=-\sum_jp_{j|i}log_2(p_{j|i})$

困惑度可以解释为一个点附近的有效邻近点个数。SNE对困惑度的调整比较有鲁棒性，通常选择5-50之间，给定之后寻找合适的$\sigma$

核心问题是如何求解梯度，目标函数等价于$\sum\sum-plog(p)$这个式子与softmax非常相似，softmax的目标函数是$\sum-ylogp$，对应的梯度是y-p（注：这里的softmax中y表示label,p表示预估值）。同样我们可以推导SNE的目标函数中的i在j的条件概率情况的梯度是2$(p_{i|j}-q_{i|j})(y_i-y_j)$,同样j在i的条件概率的梯度是2$(p_{j|i}-q_{j|i})(y_i-y_j)$，最后得到完整的梯度公式：

$\frac{\partial C}{\partial y_i}=2\sum_j(p_{j|i}-q_{j|i}+p_{i|j}-q_{i|j})(y_i-y_j)$

初始化时，可以用较小的$\sigma$下的高斯分布来进行初始化。为了加速优化过程和避免陷入局部最优解，梯度中需要使用一个相对较大的动量（momentum）.即参数更新中除了当前的梯度还要引入之前的梯度累加的指数衰减项，如下：

$Y^{(t)}=Y^{(t-1)}\eta \frac{ \partial C}{\partial Y}+α(t)(Y^{(t-1)}-Y^{(t-2)})$

这里的$Y^{(t)}$表示迭代t次的解，$\eta$表示学习速率，α(t)表示迭代t次的动量。

此外，在初始化的阶段每次迭代中可以引入一些高斯噪声，之后像模拟退火一样逐渐减小该噪声，可以用来避免陷入局部最优解。因此，SNE在选择高斯噪声，以及学习噪声，什么时候开始衰减，动量选择等等超参数上，需要跑多次优化才可以。

t-SNE原理推导

尽管SNE提供了很好的可视化方法，但他很难优化，而且存在“crowding problem”（拥挤问题）。后续Hinton等人提出了t-SNE.

与SNE不同，主要如下：

1.使用对称版的SNE，简化梯度公式
2.低维空间下，使用t分布替代高斯分布表达两点之间的相似度

t-SNE在低维空间下使用更重长尾分布的t分布来避免crowding问题和优化问题。下面先介绍对称版的SNE，之后介绍crowding问题，之后再介绍t-SNE.

Symmetric SNE

优化$p_{i|j}$和$q_{i|j}$的KL散度的一种替换思路是，使用联合概率分布来替换条件概率分布，即P是高维空间里各个点的联合概率分布，Q是低维空间下的，目标函数为

$C=KL(P||Q)=\sum_{i}\sum_{j}p_{i,j}log\frac{p_{ij}}{q_{ij}}$

这里$p_{ii},q_{ii}$为0，我们将这种SNE称之为Symmetric SNE（对称SNE）,因为他假设了对于任意i,$p_{ij}=p_{ji}$，$q_{ij}=q_{ji}$,因此概率分布可以改写为：

$p_{ij}=\frac{exp(-||x_i-x_j||^2/2\sigma^2)}{\sum_{k≠l}exp(-||x_{k}-x_{l}||^2/2\sigma^2)}$

$q_{ij}=\frac{exp(-||y_i-y_j||^2)}{\sum_{k≠l}exp(-||y_k-y_l||^2)}$

这种表达方式，使得整体简洁了很多。但是会引入异常值的问题。如果$x_i$是异常值，那么$||x_i-x_j||^2$会很大，对应的所有的j，$p_{ij}$很小（之前是仅在$x_i$下很小），导致低维映射下的$y_i$对cost影响很小。

为了解决这个问题，我们将联合概率分布定义修正为$p_{ij}=\frac{p_{i|j}+p_{j|i}}{2}$,这保证了$\sum_{j}p_{ij}>\frac{1}{2n}$,使得每个点对于cost都会有一定的贡献。对称SNE的最大优点是梯度计算变得简单了，如下：

$\frac{\partial C}{\partial y_i}=4\sum_j(p_{ij}-q_{ij})(y_i-y_j)$

实验中，发现对称SNE能够产生和SNE一样好的结果，有时甚至略好一点。

crowding问题

拥挤问题就是说各个簇聚集在一起，无法区分。比如有一种情况，高维度数据在降维到10维下，可以有很好的表达，但是降维到两维后无法得到可信映射，比如降维如10维中有11个点之间两两等距离的，在二维下就无法得到可信的映射结果（最多3个点）。进一步的说明，假设一个以数据点$x_i$为中心，半径为r的m维球（三维空间就是球），其体积是按$r^m$增长的，假设数据点是在m维球中均匀分布，我们来看看其他数据点与$x_i$的距离随维度增大而产生的变化。

如何解决crowding问题呢？？
Cook et al(2007)提出一种slight repulsion的方式，在基线概率分布中引入一个较小的混合因子$\rho$,这样$q_{ij}$就永远不会小于$\frac{2\rho}{n(n-1)}$（因为一共了n(n-1)个pairs）,这样在高维空间中比较远的两个点之间的$q_{ij}$总会比$p_{ij}$大一点。这种称之为UNI-SNE,效果通常比标准的SNE要好。优化UNI-SNE的方法是让$\rho$为0，使用标准的SNE优化，之后用模拟退火的方法的时候，再慢慢增加$\rho$，直接优化UNI-SNE是不行的（即一开始$\rho$不为0），因为距离远的两个点基本是一样的$q_{ij}$(等于基线分布)，即使$p_{ij}$很大，一些距离变化很难在$q_{ij}$中产生作用。也就是说优化中刚开始距离较远的两个聚类点，后续就无法再把他们拉近了。

t-SNE

对称SNE实际上在高维度下，另外一种减轻“拥挤问题”的方法：在高维空间下，在高维空间下我们使用高斯分布将距离转换为概率分布，在低维空间下，我们使用更加偏重长尾分布的方式来将距离转换为概率分布，使得高维度下中低等的距离在映射后能够有一个较大的距离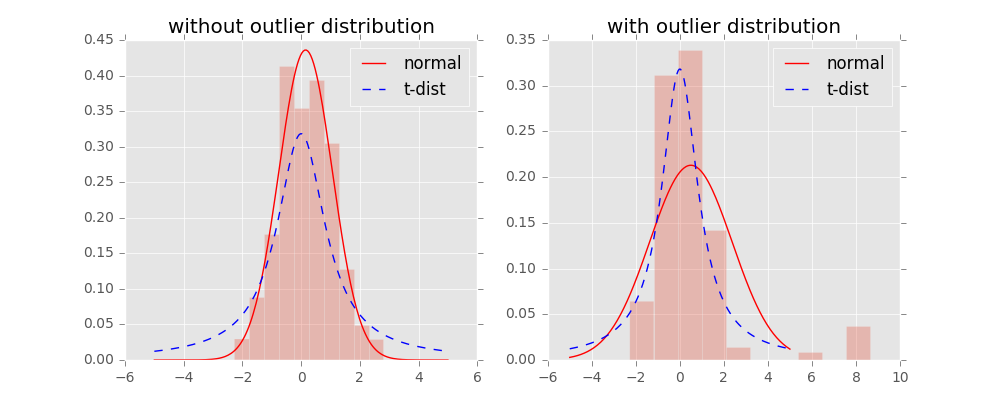
t-SNE_1
我们对比一下高斯分布和t分布(如上图)。可以看到，t分布受异常值影响更小，拟合结果更为合理，较好的捕获了数据的整体特征。
使用了t分布之后的q变化，如下：

$q_{ij}=\frac{(1+||y_i-y_j||^2)^{-1}}{\sum_{k≠l}(1+||y_i-y_j||^2)^{-1}}$

此外，t分布是无限多个高斯分布的叠加，计算上不是指数的，会方便很多。优化的梯度如下：

$\frac{\partial C}{\partial y_i}=4\sum_j(p_{ij}-q_{ij})(y_i-y_j)(1+||y_i-y_j||^2)^{-1}$

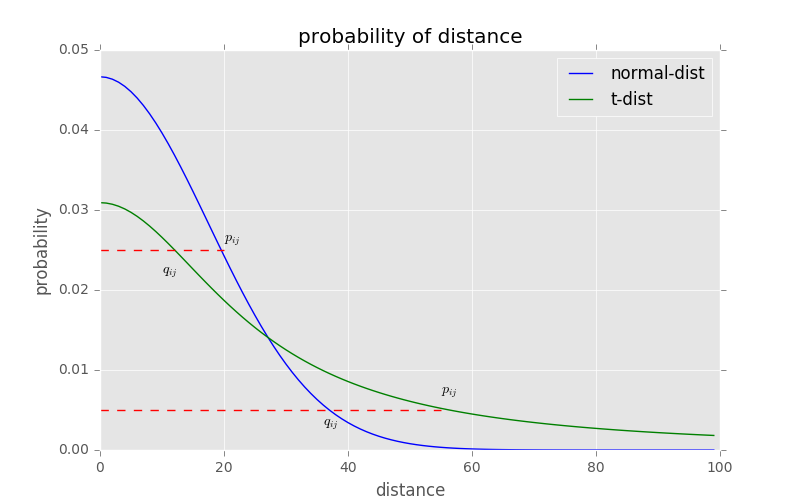
t-SNE_2
t-SNE的有效性，也可以从上图中看到：横轴表示距离，从纵轴表示相似度，可以看到，对于较大相似度的点，t分布在低维空间中的距离需要稍微小一点；而对于低相似度的点，t分布在低维空间中的距离需要更远。这恰好满足了我们的需求，即同一簇内的点(距离较近)聚合的更紧密，不同簇之间的点(距离较远)更加疏远。