优化算法

第一次接触优化算法应该是在学习数值分析的时候，但是有什么梯度下降法，牛顿下降法，拟牛顿法等一些方法。之后就是在深度学习中看到一些奇怪的优化算法，这里主要是就介绍深度学习中的优化算法。

梯度下降

其实梯度下降可以分为好多种：
（1）Batch gradient descent(BGD)：最小化所有训练样本的损失函数。这就表明其是向着全局损失函数最优的方向去。每一步迭代，都要用到训练集所有的数据。显然，在依靠大数据支撑的深度学习中，这种方法会使迭代速度变慢。
（2）Stochastic gradient descent(SGD):最普遍听到的一种梯度下降，他会最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局损失函数最优方向，但是大的整体方向是与全局最优一致的。最终结果往往是在全局最优解附近。通过每个样本来迭代更新，显然如果样本数据量大，也是会减慢速度的。SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优方向。但是相较于BGD,SGD更容易从一个local minimum跳到另一个local minimum(但是当learning rate过小时，performance便和BGD相似)；High variance,更容易使得loss curve 产生振荡。
（3）Mini-batch gradient descent：计算整个训练集的某个自己的梯度，然后更新梯度。结合SGD和BGD两者的优势，同时也弥补了两者的缺点。比SGD更稳定，更易收敛；比BGD速度更快，计算量要小。

这里我们在深度学习中常提到的SGD就是MGD（即对批样本的处理）

这里从统计学角度来考虑，一个batch里的样本损失函数的梯度与BGD里所有样本的损失函数的梯度相比，应该还是存在着点偏差。如何缓解这个问题？？

引入Momentum

引入Momentum来缓解上述问题。Momentum借用物理中的动量的概念，即前几次的梯度也参与运算。为了表示动量，引入了一个新的变量v(velocity).这里用v来代替了前面GD算法的梯度累加。

这里做个类比：

• 参数$\theta$好比海拔高度，他的目标是到海拔为0的山谷里
• 变量v是速度，与日常里的速度不同，该速度对应的时间是离散的，不是连续的。是我们走下坡时的速度。
• 动量m好比加速度，影响着我们的速度v

这里指定方向为向上为正，向下为负。

具体实现：
需要：学习率r，初始参数$\theta$，初始速率v,动量衰减参数α
每步迭代过程：
1.从训练集中的随机抽取一批容量为n的样本${x_1,….,x_n}$，以及相关的输出$y_i$
2.计算梯度和误差，并更新速度v和参数$\theta$

$$m=+\frac{1}{n}▽_ {\theta}\sum_iL(f(x_i;\theta),y_i)$$ $$v=αv-rm$$ $$\theta=\theta +v$$

其中α是衰减系数，有些地方也称为速度的摩擦系数。

如果每次迭代得到的梯度都是$\hat{m}$,那么最后的到的v的稳定值为$\frac{r||g||}{1-α}$,也就是说momentum最好的情况能够将学习速度加速$\frac{1}{1-α}$倍。

Nesterov动量

与普通动量不同，在理论上对于凸函数它能得到更好的收敛，实践中确实比标准动量表现更好一些。

核心思路：

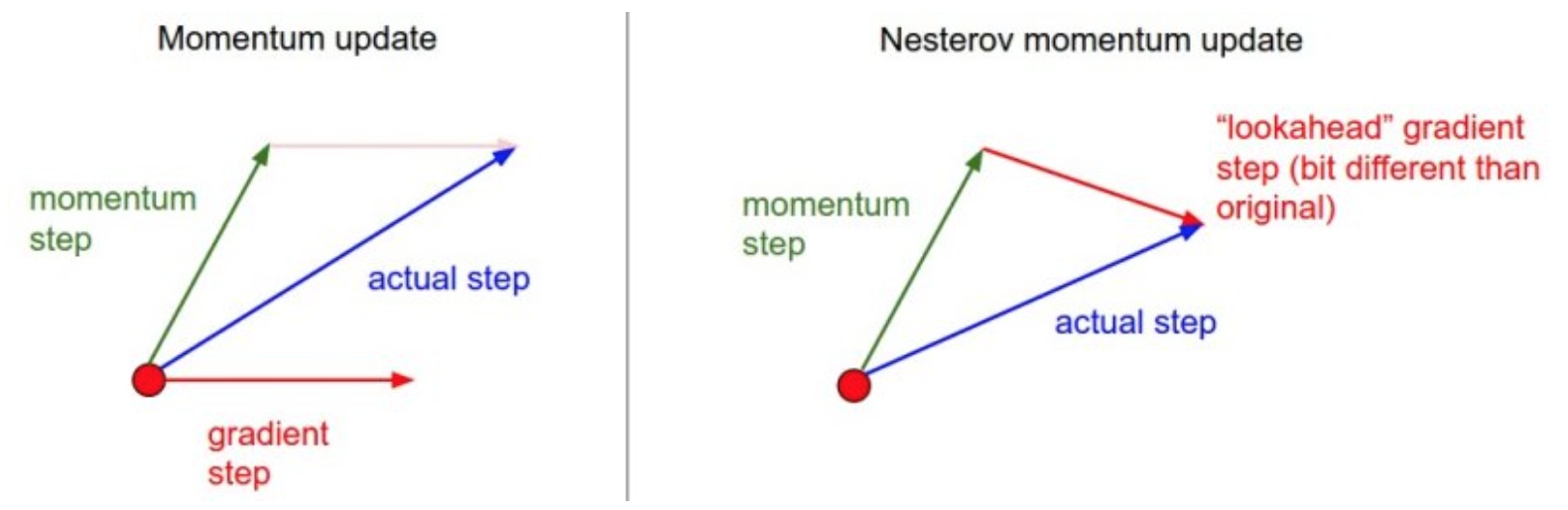
从图上可看出，前一种方法是在红点处既计算momentum step又计算gradient step，而Nesterov是在momentum step后计算该处的gradient step。
具体实现：
需要：学习率r，初始参数$\theta$,初始速率v，动量衰减参数$\theta$
每步迭代过程
1.从训练集中随机抽取一批容量为n的样本${x_1,….,x_n}$,以及相关的输出$y_i$
2.计算梯度和误差，并更新速度和参数$\theta$:

$$m=+\frac{1}{n}▽_ {\theta}\sum_iL(f(x_i;\theta+αv),y_i)$$ $$v=αv-rm$$ $$\theta=\theta+v$$

注意在估算m的时候参数变为了$\theta+αv$而不是先前的$\theta$

AdaGrad

AdaGrad可以自动变更学习速率，只是需要设定一个全局的学习速率r，但是这并非是实际学习速率，实际的速率与以往参数的模之和的开方成反比。

$$r_n=\frac{r}{\delta+\sqrt{\sum_{i=1}^{n-1}g_i^2}}$$

其中$\delta$是一个很小的常量，大概在$10^{-7}$，防止出现分母为0

具体实现：
需要：全局学习率r，初始参数$\theta$,数值稳定值$\delta$
中间变量：梯度累计量u（初始化为0）
每步迭代过程：
1.从训练集中随机抽取一批容量为n的样本${x_1,….,x_n}$,以及相关的输出$y_i$
2.计算梯度和误差，更新u，再根据u和梯度计算参数更新量。

$$m=+\frac{1}{n}▽_ {\theta}\sum_iL(f(x_i;\theta),y_i)$$ $$u=u+m^2$$ $$\Delta \theta=-\frac{r}{\delta+\sqrt{u}}m$$ $$\theta=\theta+\Delta \theta$$

刚算法只是引入了自适应的学习率，也没有用到前面的动量、速率。

优点：能够实现学习率的自动更改。前期梯度较大，后期梯度较小。
缺点：仍然要设置一个变量r

经验表明，在普通算法中也许效果不错，但在深度学习中，深度过深会造成训练提前结束。

RMSProp

对上述Adagrad算法做出改进
RMSProp通过引入一个衰减系数，让u每回合都衰减一定比例。

具体实现：
需要：全局学习率r，初始参数$\theta$，数值稳定量$\delta$，衰减速率$\rho$
中间变量：梯度累计量u（初始为0）
每步迭代过程：
1.从训练集中随机抽取一批容量为n的样本${x_1,….,x_n}$,以及相关的输出$y_i$
2.计算梯度和误差，更新u和梯度计算参数更新量

$$m=+\frac{1}{n}▽_ {\theta}\sum_iL(f(x_i;\theta),y_i)$$ $$u=\rho r+(1-\rho)m^2$$ $$\Delta \theta=-\frac{r}{\delta+\sqrt{u}}m$$ $$\theta=\theta+\Delta\theta$$

优点：
相比于Adagrad，这种方法很好的解决了深度学习中过早结束的问题，适合处理非平稳目标，对于RNN效果很好。
缺点：
又引入了新的超参，衰减系数$\rho$
依然依赖全局学习率

RMSProp with Nesterov Momentum

具体实现：
需要：全局学习率r，参数$\theta$,初始速率v，动量衰减系数α，梯度累积量衰减速率$\rho$
中间变量：梯度累计量u（初始化为0）
每步迭代过程：
1.从训练集中随机抽取一批容量为n的样本${x_1,….,x_n}$,以及相关的输出$y_i$
2.计算梯度和误差，更新u和梯度计算参数更新量

$$\hat{\theta}=\theta+αv$$ $$m=+\frac{1}{n}▽_ {\hat{\theta}}\sum_{i}L(f(x_i;\hat{\theta}),y_i)$$ $$u=\rho u+(1-\rho)m^2$$ $$v=αv-\frac{r}{\sqrt{u}}m$$ $$\theta=\theta+v$$

Adam

Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSProp,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。

具体实现：
需要：学习率r，参数$\theta$,数值稳定量$\delta$，一阶动量衰减系数$\rho_1$,二阶动量衰减系数$\rho_2$
其中几个取值一般为：$\delta=10^{-8}$,$\rho_1=0.9$,$\rho_2=0.999$
中间变量：一阶动量s,二阶动量u，都初始化为0
每步迭代过程：
1.从训练集中随机抽取一批容量为n的样本${x_1,….,x_n}$,以及相关的输出$y_i$
2.计算梯度和误差，更新u和s,再根据u和s及梯度计算参数更新量

$$m=+\frac{1}{n}▽_ {\theta}\sum_iL(f(x_i;\theta),y_i)$$ $$s=\rho_1s+(1-\rho_1)m$$ $$u=\rho_2u+(1-\rho_2)m^2$$ $$\hat{s}=\frac{s}{1-\rho_1}$$ $$\hat{u}=\frac{u}{1-\rho_2}$$ $$\Delta\theta=-r\frac{\hat{s}}{\sqrt{\hat{u}}+\delta}$$ $$\theta=\theta+\Delta\theta$$

Adamax

这是Adam的一种变体，此方法对学习率的上限提供了一个更简单的范围。公式变化如下：

$$u_t=max(\rho_2u_{t-1},|m_t|)$$ $$\Delta{x}=-\frac{\hat{s_t}}{\hat{u_t}+\epsilon}×r$$

可以看出，Adamax学习率边界范围更简单。

Nadam

类似于带有Nesterov动量项的Adam.公式如下：

$$\hat{m_t}=\frac{m_t}{1-\prod_{i=1}^{t}\rho_{1i}}$$ $$s_t=\rho_{1t} s_{t-1}+(1-\rho_{1t})m_t$$ $$\hat{s_t}=\frac{s_t}{1-\prod_{i=1}^{t+1}\rho_{1t}}$$ $$u_t=u_{t-1}\rho_2+(1-\rho_2)m_t^2$$ $$\hat{u_t}=\frac{u_t}{1-\rho_{2t}}\overline{s_t}=(1-\rho_{1t})\hat{m_t}+\rho_{1t+1}\hat{m_t}$$ $$\Delta{\theta_t}=-\eta\frac{\overline{s_t}}{\sqrt{\hat{u_t}}+\epsilon}$$

可以看到Nadam对学习率有了更强的约束，同时对梯度的更新也有更直接的影响。一般而言，在想使用带动量的RMSprop，或者Adam的地方，大多数可以使用Nadam取得更好的效果。

经验之谈

• 对于稀疏数据，尽量使用学习率可自适应的优化方法，不用手动调节，而且最好采用默认值
• SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠
• 如果在意更快的收敛，而且需要训练较深复杂的网络时，推荐使用学习率自适应的方法
• RMSprop，Adam是比较相近的算法，在相似的情况下表现差不多
• 在想使用带动量的RMSprop，或者Adam的地方，大多可以使用Nadam取得更好的效果。

参考文献

• 1.深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）