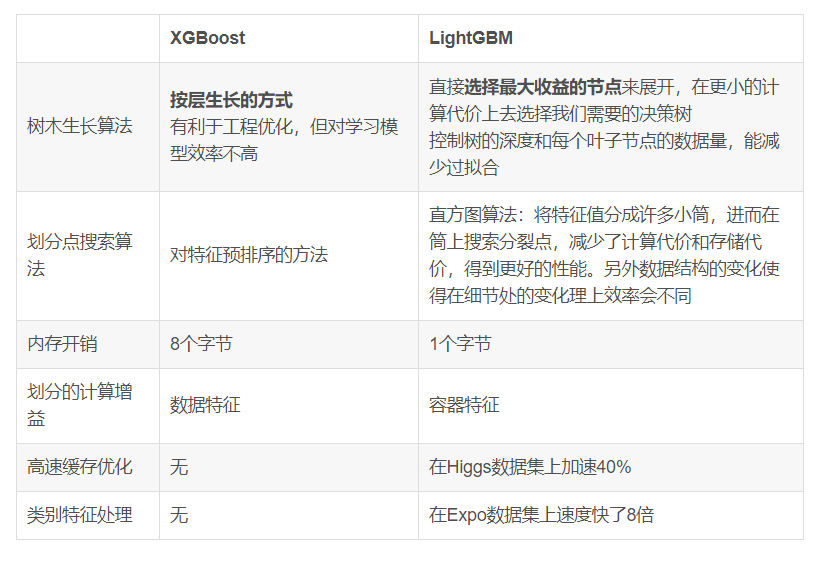
最近发现Lightgbm比XGBoost算法更加牛逼,因此整理了这份资料。
lightGBM顾名思义:light:轻量;GBM梯度提升机
XGBoost的缺点
- 每次迭代时,都需要遍历整个训练数据多次.如果把训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间
- 预排序方法(pre-sorted):空间消耗大,算法需保存数据的特征值,还保存了特征排序的结果(例如排序后的索引,为了后续快速的计算分割点),这里需要消耗训练数据的2倍内存。其次时间上也有较大开销,在遍历每一个分割点时都需要进行分裂增益的计算,消耗代价大.
- 对cache优化不友好.在预排序后,特征对梯度的访问是一种随机访问,并且不同特征访问的顺序不一样,无法对cache进行优化.
- XGboost的并行化并不是tree粒度的,而是特征粒度的,树之间仍然是串行依赖关系.
lightGBM提出两种新方法:Gradient-based One-Side Sampling(GOSS)和Exclusive Feature Bundling(EFB)
Gradient-based One-Side Sampling(GOSS)
GOSS(基于梯度的单边采样)方法的主要思想是,梯度大的样本点在信息增益的计算上扮演着重要的作用,也就是说这些梯度大的样本点会贡献更多的信息增益,因此为了保持信息增益评估的精度,当我们对样本进行下采样的时候保留这些梯度大的样本点,而对于梯度小的样本点按比例进行随机采样即可.
在AdaBoost算法中,每次迭代时更加注重上一次错分的样本点,也就是上一次错分的样本点的权重增大,而在GBDAT中没有本地的权重来实现这样的过程,所以在AdaBoost中提出的采样模型不能应用在GBDT中.但是每个样本的梯度能提供这种有效信息。
也就是说如果一个样本点梯度小也就是说它已经经过很好的训练了,所以可以抛弃它。但是这样做会改变数据的分布和损失学习的模型精度.为了避免这种情况,提出了GOSS.

解释上图:
输入:数据点I,迭代次数d,大梯度数据的采样率a,小梯度数据采样率b,loss function,L:弱学习器
迭代d次:
- 根据样本点的梯度的绝对值进行降序排序
- 对排序后的结果选取a×100%的样本生成一个大梯度样本点的子集
- 对剩下的样本集合(1-a)×100%的样本,随机的选取b×(1-a)×100% 个样本点,生成一个小梯度样本点的集合;
- 将大梯度样本和采样的小梯度样本合并
- 将小梯度样本乘上一个权重系数$\frac{1-a}{b}$
- 使用上述的采样的样本,学习一个新的弱学习器
- 不断重复上述步骤直到达到规定迭代次数或者收敛为止
已知当a=0时,GOSS算法退化为随机采样算法;当a=1时,GOSS算法变为采取整个样本的算法。在许多情况下,GOSS算法训练出的模型精度高于随机采样算法。另一方面,采样也就会增加弱学习器的多样性,从而潜在地提升训练出地模型泛化能力
Exclusive Feature Bundling(EFB)
LightBGM不仅进行了数据采样,也进行了特征抽取.使模型的训练速度进一步地减少.但是该特征抽取又与一般的特征抽取不同,是将互斥特征绑定在一起从而减少特征维度.这主要思想:通常在实际应用中高纬度的数据往往都是系数数据,这使我们有可能设计一种几乎无损的方法来减少有效特征的数量.尤其,在稀疏特征空间中许多特征都是互斥的(例如很少同时出现非零).这使我们可以安全地将互斥特征绑定在一起形成一个特征,从而减少特征维度.但是怎样的将互斥特征绑定在一起?LightGBM作者使用的是基于直方图:
互斥特征绑定(EFB)算法
注意:这里互斥的定义:很少同时出现非零的两个特征
解释上图:
输入:特征F,最大冲突数K
- 构造一个边带有权重的图,其权重对应于特征之间的总冲突数
- 通过特征在图中度来降序排序特征
- 检查有序列表中的每个特征,并将其分配给具有小冲突的现有bunding(由K控制或创建新的bunding)
上述算法的时间复杂度是$O(#feature^2)$,并且在模型训练之前仅仅被处理一次即可.在特征维度不是很大时,这样复杂度是可以接受的.担当特征维度较高时,这种方法就会特别的低效.因此作者又提出一种更高效的算法,按非零值的计数排序,这类似于按度数排序,因为更多的非零值通常会导致更高的冲突概率.这仅仅改变上述算法的排序策略,所以只是针对上述算法将按度数排序改为按非0值数量排序,其他不变
如何合并互斥特征?
Lightgbm关于互斥特征的合并用到了直方图(Histogram)算法.直方图算法的基本思想是把连续的特征值离散化成k个整数,同时构造一个宽度为k的直方图.在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优分割点.
由于基于直方图的算法存储的是离散点的bins而不是连续的特征值,我们可以通过让互斥特征驻留在不同的bins中来构造feture bundle.这可以增加特征原始值的偏移量来实现.比如,假设我们有两个特征,特征A的取值范围为[0,10],特征B的取值范围是[0.20];我们可以给特征B增加偏移量10,使得特征B的取值范围为[10,30),最后合并特征A和B,形成新的特征范围为[0,30)来取代特征A和特征B
由于特征被离散化后,找到的并不是精确的分割点,所以会对结果产生影响.但我们的决策树本来就是弱分类器,因此分割点的不是很精确并不是太重要.而且这样也会有正则化的效果.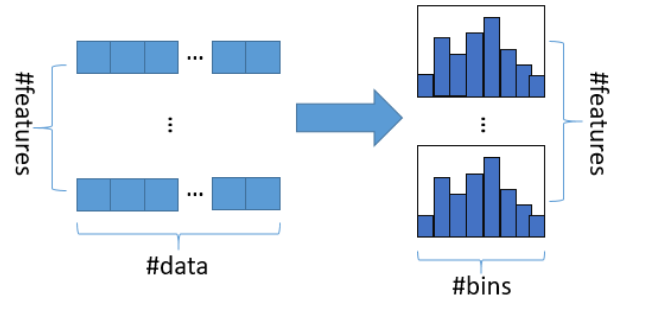

Histogram算法的优点:
LightBGM
LightBGM就是使用了GOSS和EFB的GBDT.
Lightgbm的决策树生长策略:
大部分决策树的学习算法通过level-wise 策略生长树,即一次分裂同一层的叶子,不加区分的对待同一层的叶子,而实际上很多叶子的分裂增益比较低没必要进行分裂,带来了没必要的开销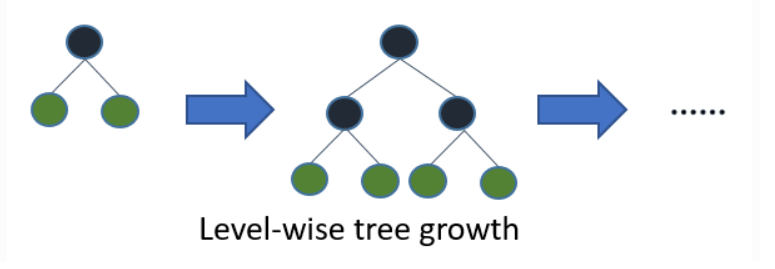
LightGBM通过leaf-wise策略来生长树.每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后进行分裂,如此循环.因此同Level-wise相比,在分裂次数相同地情况下,Leaf-wise可以降低更多的误差,得到更好的精度.但是,当样本量较小的时候,leaf-wise可能会造成过拟合.所以,LightGBM可以利用额外的max_depth来限制树的深度从而避免过拟合.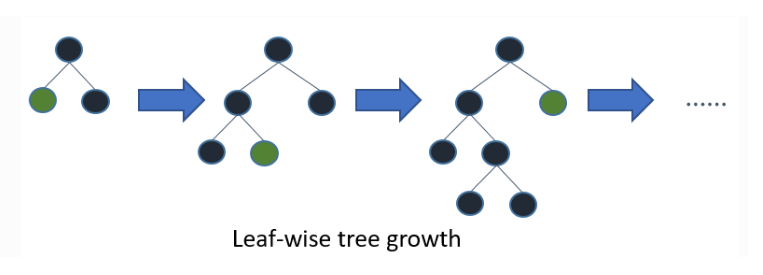
Lightgbm的并行学习:
- 特征并行
- 数据并行
- 投票并行
LightBGM与XGBoost的比较