数据清洗与预处理汇总

发表于 | 分类于 | 阅读数 次
字数统计: 4.2k 字 | 阅读时长 ≈ 16 分钟

直观上来看,一个项目的流程可以用下图来表示: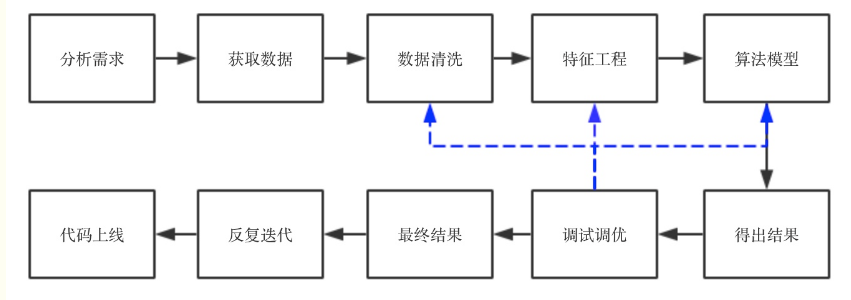
pic1
从上图可以看出,数据清洗是一个需要重复进行调整的过程.在整个流程中占据举足轻重的作用.当然从图上也可看出,特征工程和算法模型也很重要.

查看并分析数据

拿到数据之后,首先需要对数据进行描述性统计分析,查看哪些数据是不合理的,也可以了解数据的基本情况.这里可以用pandas库里的函数进行分析.

pic2
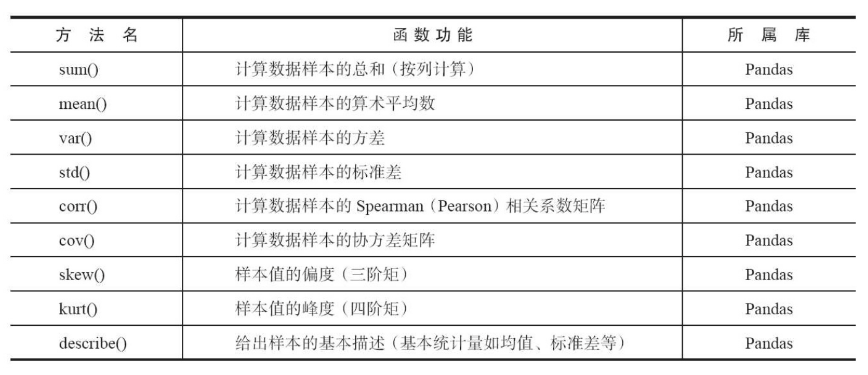
上面是pandas中常用的一些方法,可以进行数据统计.

数据清洗

在分析数据之后,我们可以看出数据有哪些特点,以及数据有哪些缺点.
我们这里的数据清洗是将重复、多余的数据筛选清楚,将缺失的数据补充完整,将错误的数据纠正或者删除,最后整理成为我们可以进一步加工、使用的数据.

选择正确的方式来清洗数据极为重要.

数据清洗的一般步骤:分析数据、缺失值处理、异常值处理、去重处理、噪音数据处理

缺失值处理

缺失值就是常常就是在数据中用nan表示的值.

1
2
3
import numpy as np
data=np.genfromtxt("web_traffic.tsv",delimiter="\t")#读取文件,并以"\t"分割
print(data)

  1. 若缺失值并没有很多,可以考虑删除它们,因为删除后对整体数据影响不大.

  2. 使用一个全局常量填充 ——譬如将缺失值用”Unknown”等填充,但是效果不一定好,因为,因为算法可能会把它识别为一个新的类别,一般很少用

  3. 使用均值或中位数代替——优点:不会减少样本信息,处理简单.缺点:当缺失数据不是随机数据时会产生偏差.对于正常分布的数据可以使用均值代替,如果数据是倾斜的,使用中位数可能更好
    sklearn里的imputer可以用于填充

    1
    2
    3
    from sklearn.preprocessing import Imputer
    imputer=Imputer(missing_values=np.nan,strategy='mean',axis=0)#均值填充
    X[:,1:3]=imputer.fit_transform(X[:,1:3])

Imputer参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.proprecessing import Imputer

填补缺失值：sklearn.preprocessing.Imputer(missing_values=’NaN’, strategy=’mean’, axis=0, verbose=0, copy=True)

主要参数说明：

missing_values：缺失值，可以为整数或NaN(缺失值numpy.nan用字符串‘NaN’表示)，默认为NaN

strategy：替换策略，字符串，默认用均值‘mean’替换

①若为mean时，用特征列的均值替换

②若为median时，用特征列的中位数替换

③若为most_frequent时，用特征列的众数替换

axis：指定轴数，默认axis=0代表列，axis=1代表行

copy：设置为True代表不在原数据集上修改，设置为False时，就地修改，存在如下情况时，即使设置为False时，也不会就地修改

  1. 插补法:
    1) 随机插补法：从总体中随机抽取某个样本代替缺失样本
    2)多重插补法:通过变量之间的关系对缺失数据进行预测,利用蒙特卡洛方法生成多个完整的数据集,在对这些数据集进行分析,最后对分析结果进行汇总处理.
    3)热平台插补:指在非缺失数据集中找到一个与缺失值所在样本相似的样本(匹配样本),利用其中的观测值对缺失值进行插补
  • 优点：简单易行,准取率较高
  • 缺点：变量数量较多时,通常很难找到与需要插补样本完全相同的样本.但我们可以按照某些变量将数据分层,在层中对缺失值实用均值插补
    4)拉格朗日差值法和牛顿插值法
  1. 可以用回归、实用贝叶斯形式化方法的基于推断的工具或决策树归纳确定.例如,利用数据集中其他数据的属性,可以构造一棵判定树,来预测缺失值的值.

以上方法各有优缺点，具体情况要根据实际数据分分布情况、倾斜程度、缺失值所占比例等等来选择方法。一般而言，建模法是比较常用的方法，它根据已有的值来预测缺失值，准确率更高。

异常值处理

异常值也就是我们常说的”离群点”.如何发现离群点?

  1. 箱型图分析
    之前在统计学的文章中有介绍过箱型图可以发掘离群点.

  2. 3$\sigma$
    在3$\sigma$原则下,异常值为一组测定值中与平均值的偏差超过3倍标准差的值.如果数据服从正态分布,距离平均值$3\sigma$之外的值出现的概率为$P(|x-\mu|＞3\sigma)≤0.003$,术语极个别的小概率事件.如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述.

  3. 基于模型检测
    首先建立一个数据模型,异常是那些同模型不能完美拟合的对象;如果模型是簇的集合,异常就是不显著属于任何簇的对象;在实用回归模型时,异常值是对远离预测值的对象.

  4. 基于距离
    通常可以在对象之间定义邻近性度量,异常对象是那些远离其他对象的对象
    缺点:基于近邻度的方法需要$O(m^2)$的事件,不适合大数据
  5. 基于密度
    当一个点的局部密度显著低于它的大部分近邻时才将其分类为离群点,适合非均匀分布的数据.
  6. 基于聚类
    基于聚类的离群点:一个对象是基于聚类的离群点,如果该对象不强属于任何簇.离群点对初始聚类的的影响:如果通过聚类检测离群点,则由于离群点影响聚类,存在一个问题:结构是否有效.为了处理该问题,可以使用如下方法：对象聚类,删除离群点,对象再次聚类(这个不能保证产生最优结果).

发现了异常值以后我们要想办法处理它们,处理方法有:

  1. 删除异常值——明显看出是异常且数量较少可以直接删除
  2. 不处理——如果算法对异常值不敏感则可以不处理,但如果算法对异常值敏感,则最好不要用,如基于距离计算的一些算法,包括k-means,knn之类的.
  3. 平均值替代——损失信息小,简单高效
  4. 视为缺失值——可以按照处理缺失值的方法来处理

    sklearn

    清洗数据有时会需要用来检测新观测数据是否与已有数据服从同一分布(若不服从则可能是异常值)
    存在两类检测:
  • Novelty Detection:训练数据中没有离群点,我们是对检测新发现的样本点感兴趣
  • outlier Detection:训练数据中包含离群点,我们需要适配训练数据中的中心部分(密集的部分),忽视异常点;

Novelty Detection:
样本数n;特征数p;待测样本1个.
主要是用来判断待测样本是不是符合原来数据的分布.这里用的是OneClassSVM,进行分类.
例子:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn import svm

xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# Generate train data
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]  # 全是正常的，预测值应为1
# Generate some regular novel observations
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]  # 全是正常的，预测值应为1
# Generate some abnormal novel observations
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))  # 全是异常的，预测值应为-1

# fit the model
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)  # 训练集的标签
y_pred_test = clf.predict(X_test)  # 正常测试集的标签
y_pred_outliers = clf.predict(X_outliers)  # 异常测试集的标签
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size

# plot the line, the points, and the nearest vectors to the plane
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.title("Novelty Detection")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')

s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s)
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s)
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s)
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a.collections[0], b1, b2, c],
           ["learned frontier", "training observations",
            "new regular observations", "new abnormal observations"],
           loc="upper left",
           prop=matplotlib.font_manager.FontProperties(size=11))
plt.xlabel(
    "error train: %d/200 ; errors novel regular: %d/40 ; "
    "errors novel abnormal: %d/40"
    % (n_error_train, n_error_test, n_error_outliers))
plt.show()

传统的SVM是二分类的,而这里的One-Class SVM是分成一个类和不是这个类的(不会给出明确的类).很适合这里检测异常值.

异常点检测(outlier Detection):
异常点检测与前面有相同的目的,都是为了把大部分数据聚集的簇与少量的噪声样本点分开.不同的是,对于异常点检测来说,我们手上的训练集并不干净.
存在4种方法:

  1. Fitting an elliptic envelope:
    假设常规数据隐含着一个已知的概率分布.基于这个假设,我们确定数据的形状(边界)，可以将远离边界的样本点定义为异常点.Sklearn提供的convariance.EllipticEnvelope类,它可以根据数据做一个鲁棒的协方差估计,然后学习到一个包围中心样本点并忽视离群点的椭圆.
  2. Isolation Forest
    孤立森林是一个高效的异常点监测算法.sklearn提供了ensemble.IsolationForest模块.该模块在进行检测时会随机选取一个特征,然后再所选特征的最大值和最小值随机选择一个分切面.该算法下整个训练集的训练就像一棵树一样,递归的划分.划分的次数等于根节点到叶子结点的路径距离d.所有随机树(为了增强鲁棒性,会随机选取很多树形成森林)的d的平均值,就是我们检测函数的最终结果.那些路径d比较小的,都是因为距离主要的样本点分布中心较远的.也就是说可以通过寻找最短路径的叶子结点来寻找异常点.(之所以是最短的,因为距离长的说明它与大部分数据堆在一起不容易区分开)
    1. One-class SVM
      严格来说，一分类的SVM并不是一个异常点监测算法，而是一个奇异点检测算法
    2. LocalOutlierFactor(LOC)
      基于密度的算法,其核心部分是关于数据点密度的刻画.(有点类似DBSCAN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
#异常检测demo
import time

import numpy as np
import matplotlib
import matplotlib.pyplot as plt

from sklearn import svm
from sklearn.datasets import make_moons, make_blobs
from sklearn.covariance import EllipticEnvelope
from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor

print(__doc__)

matplotlib.rcParams['contour.negative_linestyle'] = 'solid'

# Example settings
n_samples = 300
outliers_fraction = 0.15
n_outliers = int(outliers_fraction * n_samples)
n_inliers = n_samples - n_outliers

# define outlier/anomaly detection methods to be compared
# 四种异常检测算法，之后的文章详细介绍
anomaly_algorithms = [
    ("Robust covariance", EllipticEnvelope(contamination=outliers_fraction)),
    ("One-Class SVM", svm.OneClassSVM(nu=outliers_fraction, kernel="rbf",
                                      gamma=0.1)),
    ("Isolation Forest", IsolationForest(contamination=outliers_fraction,
                                         random_state=42)),
    ("Local Outlier Factor", LocalOutlierFactor(
        n_neighbors=35, contamination=outliers_fraction))]

# Define datasets
blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)
datasets = [
    # make_blobes用于生成聚类数据。centers表示聚类中心，cluster_std表示聚类数据方差。返回值(数据, 类别)
    # **用于传递dict key-value参数，*用于传递元组不定数量参数。
    make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5,
               **blobs_params)[0],
    make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5],
               **blobs_params)[0],
    make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, .3],
               **blobs_params)[0],

    # make_moons用于生成月亮形数据。返回值数据(x, y)
    4. * (make_moons(n_samples=n_samples, noise=.05, random_state=0)[0] -
          np.array([0.5, 0.25])),
    14. * (np.random.RandomState(42).rand(n_samples, 2) - 0.5)]

# Compare given classifiers under given settings
# np.meshgrid生产成网格数据
# 如输入x = [0, 1, 2, 3] y = [0, 1, 2]，则输出
# xx 0 1 2 3   yy 0 0 0 0
#    0 1 2 3      1 1 1 1
#    0 1 2 3      2 2 2 2
xx, yy = np.meshgrid(np.linspace(-7, 7, 150),
                     np.linspace(-7, 7, 150))

# figure生成画布，subplots_adjust子图的间距调整，左边距，右边距，下边距，上边距，列间距，行间距
plt.figure(figsize=(len(anomaly_algorithms) * 2 + 3, 12.5))
plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05,
                    hspace=.01)

plot_num = 1
rng = np.random.RandomState(42)

for i_dataset, X in enumerate(datasets):
    # Add outliers
    # np.concatenate数组拼接。axis=0行增加，axis=1列增加（对应行拼接）。
    X = np.concatenate([X, rng.uniform(low=-6, high=6,
                       size=(n_outliers, 2))], axis=0)

    for name, algorithm in anomaly_algorithms:
        t0 = time.time()
        # 专门用于评估执行时间，无用代码
        algorithm.fit(X)
        t1 = time.time()
        # 定位子图位置。参数：列，行，序号
        plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)
        if i_dataset == 0:
            plt.title(name, size=18)

        # fit the data and tag outliers
        # 训练与预测
        if name == "Local Outlier Factor":
            y_pred = algorithm.fit_predict(X)
        else:
            y_pred = algorithm.fit(X).predict(X)

        # plot the levels lines and the points
        # 用训练的模型预测网格数据点，主要是要得到聚类模型边缘
        if name != "Local Outlier Factor":  # LOF does not implement predict
            # ravel()多维数组平铺为一维数组。np.c_ cloumn列连接，np.r_ row行连接。
            Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
            # reshape这里把一维数组转化为二维数组
            Z = Z.reshape(xx.shape)
            # plt.contour画等高线。Z表示对应点类别，可以理解为不同的高度，plt.contour就是要画出不同高度间的分界线。
            plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='black')

        colors = np.array(['#377eb8', '#ff7f00'])
        plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])

        # x轴范围
        plt.xlim(-7, 7)
        plt.ylim(-7, 7)
        # x轴坐标
        plt.xticks(())
        plt.yticks(())
        # 坐标图上显示的文字
        plt.text(.99, .01, ('%.2fs' % (t1 - t0)).lstrip('0'),
                 transform=plt.gca().transAxes, size=15,
                 horizontalalignment='right')
        plot_num += 1

plt.show()

去重处理

数据库中属性值相同的记录被认为是重复记录,通过判断记录记录间的属性值是否相等来检测记录是否相等,相等的记录合并为一条记录(即合并/清除),合并/清除是消重的基本方法.

pandas中可用.duplicated()表示找出重复的行,默认是判断全部列.返回布尔类型的结果.对于完全没有重复的行,返回False,对于有重复的行,第一次出现的那一行返回False,其余的返回True

也有.drop_duplicates()来去掉重复行.

也可以指定某列判断是否有重复值.duplicated(‘name’),根据指定某列去除重复行.drop_duplicates(‘name’)

噪音处理

什么是噪音？
噪音是被测量变量的随机误差或方差.注意:离群点与噪音不是一回事儿.观测值=真实数据+噪音.离群点属于观测值,既可能是真实数据造成的,也可能是噪声造成的.噪音包括错误值或偏离期望的孤立值,但也不能说噪声点包含离群点.

如果数据中含有大量的噪声数据,将会大大的影响数据的收敛速度,甚至对于训练生成模型的准确也会有很大的副作用.

对于噪音我们应该如何处理呢？y有以下几种方法：

  1. 分箱法：
    分箱方法通过考察数据的”近邻”(即,周围的值)来光滑有序数据值.这些有序的值被分布到一些”桶”或箱中.由于分箱法考察近邻的值,因此它进行局部光滑.
  • 用箱均值光滑:箱中的每一个值被箱中的平均值替换
  • 用箱中位数平滑:箱中的每一个值被箱中的中位数替换
  • 用箱边界平滑:箱中的最大和最小值同样被视为边界.箱中的每一个值被最近的边界值替换.
    一般而言,宽度越大,光滑效果越明显.箱也可以是等宽的,其中每个箱值的区间范围是个常量.分箱也可以作为一种离散化技术使用.
  1. 回归法
    可以用一个函数拟合数据来光滑数据。线性回归涉及找出拟合两个属性（或变量）的“最佳”直线，使得一个属性能够预测另一个。多线性回归是线性回归的扩展，它涉及多于两个属性，并且数据拟合到一个多维面。使用回归，找出适合数据的数学方程式，能够帮助消除噪声。

参考文献

  1. https://www.cnblogs.com/charlotte77/p/5606926.html
-------------本文结束感谢您的阅读-------------