时间序列相关算法与分析步骤(转)

发表于 | 分类于 | 阅读数 1118次
字数统计: 1.5k 字 | 阅读时长 ≈ 5 分钟

转自：https://blog.csdn.net/omnispace?t=1

时间序列相关算法与分析步骤

从时间的相关性角度可以把一个序列基本分为3类:

  1. 纯随机序列(白噪声序列):这时候可以停止分析，因为就像预测下一次硬币哪一面朝上一样毫无规律。
  2. 平稳非白噪声序列:它们的均值和方差是常数,对于这类序列,有成熟的模型来拟合这个序列在未来的发展状况,如AR,MA,ARMA等
  3. 非平稳序列:一般做法是把他们转化为平稳的序列，在按照平稳序列的算法进行拟合。如果经过差分后平稳，则应使用ARIMA模型进行拟合。
1
注：本文模型采用的数据为某餐厅一个多月内的销量数据，包含两个特征：时间和销量

Q1:序列的平稳性用什么来衡量呢？

方法1：

根据时序图和自相关图的特征做出主观的判断，如下图：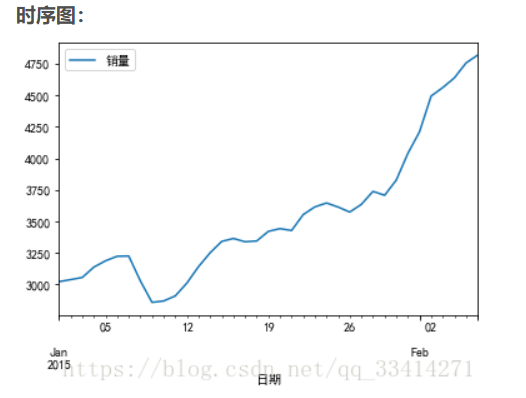
pic1
自相关图: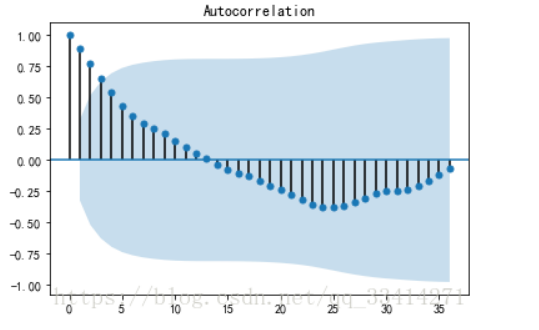
pic2
从上图可以基本看出，自相关系数的绝对值长期都保持了较大的值，所以可以判断上述时间序列存在自相关性。

平稳的序列自相关图和偏自相关图不是拖尾就是截尾。
截尾就是在某阶之后,系数都为0.
拖尾就是有一个衰减的趋势,但是不都为0.

从自相关图来看，呈现三角对称形式，不存在截尾或拖尾，属于单调序列的典型表现形式，原始数据属于不平稳序列。
注:

  1. 如果自相关是拖尾，偏相关截尾，则用 AR 算法
  2. 如果自相关截尾，偏相关拖尾，则用 MA 算法
  3. 如果自相关和偏相关都是拖尾，则用 ARMA 算法， ARIMA 是 ARMA 算法的扩展版，用法类似 。

相关系数的计算方法:

Var表示方差

方法2:

根据单位根检验
如果存在单位根，则此序列为随机非平稳序列

Q2:平稳序列应该怎么分析?

目前最常用的拟合平稳序列的模型为ARMA（Autoregressive moving average）模型，全称是自回归移动平均模型，他又可以分为AR模型，MA模型和ARMA模型三大类。

  1. 自回归AR(p)模型
  2. 移动平均MA(q)模型
  3. ARMA(p,q)模型
    ARMA(p,q)模型中包含了p个自回归项和q个移动平均项,ARMA(p,q)模型可以表示为:

一般分析步骤: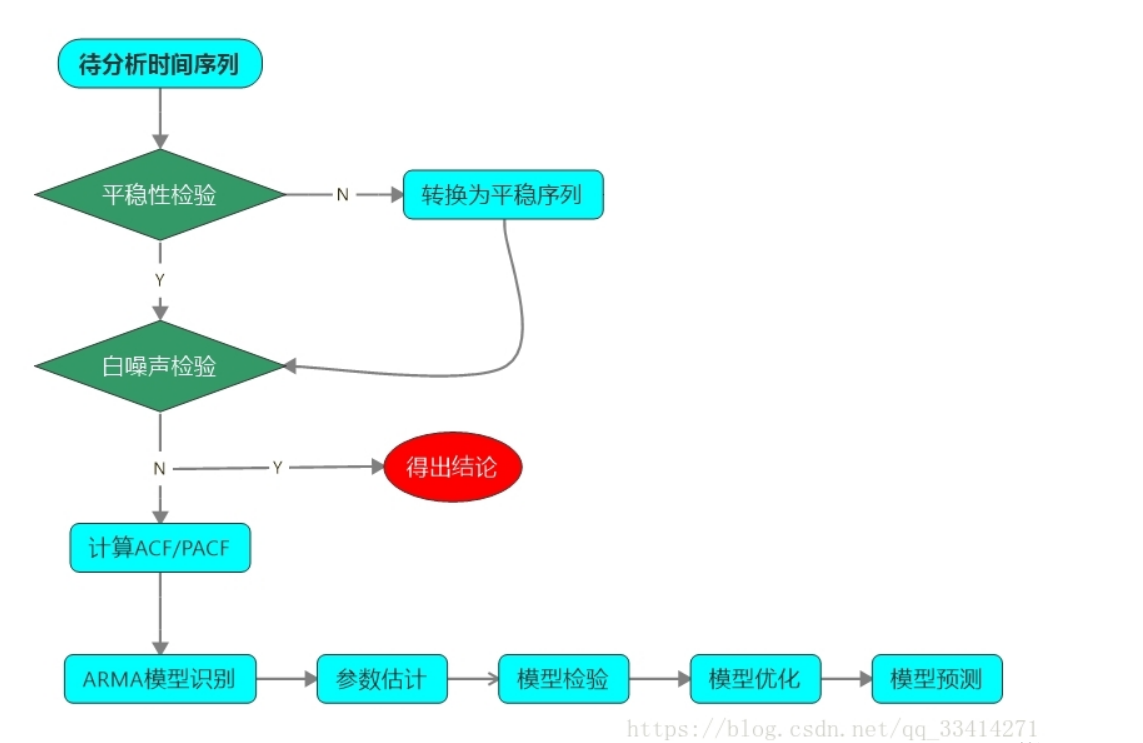
pic3

Q3:非平稳序列怎么分析呢？

从上面的模型中可以看出，如果是非平稳序列，我们需要先把它转为平稳序列之后再进行分析。
一般我们使用ARIMA(Autoregressive Integrated Moving Average model)进行分析
ARIMA（p，d，q）中，AR是”自回归”，p为自回归项数；MA为”滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。
“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

Q4:举个例子:
读取数据

1
2
3
4
5
6
7
8
9
10
11
#-*- coding: utf-8 -*-
#arima时序模型

import pandas as pd

#参数初始化
discfile = '../data/arima_data.xls'
forecastnum = 5

#读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(discfile, index_col = u'日期')

自相关检测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
data.plot()
plt.show()

#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()

#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为：', ADF(data[u'销量']))
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、

自相关图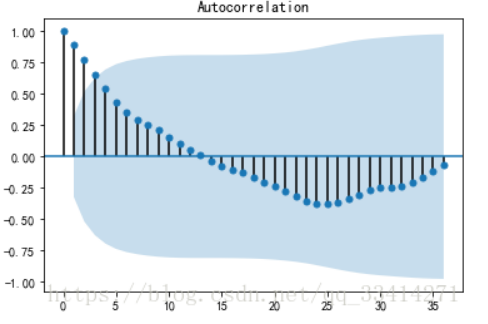
pic4

可以看出自相关系数的绝对值长期都保持很大，多以基本判断存在自相关性。
ADF检测结果p值显著大于0.05（p=0.9983），最终判断为非平稳序列

一阶差分后继续检测

1
2
3
4
5
6
7
8
9
10
11
12
13
#差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #时序图
plt.show()
plot_acf(D_data).show() #自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show() #偏自相关图
print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分'])) #平稳性检测

#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) #返回统计量和p值

pic5
pic6

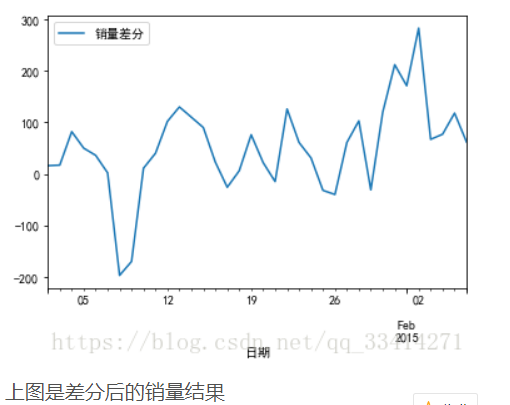
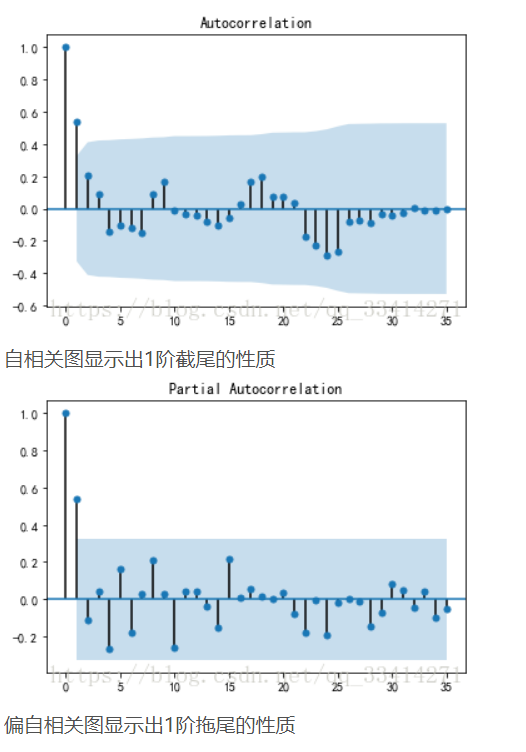
从ADF的结果（p=0.0226）和自相关图以及偏自相关图中可以看出一阶差分后的序列是平稳的非白噪声序列。

给ARIMA模型定阶
从一阶差分后的序列是平稳的非白噪声序列可以看出ARIMA模型中的d=1

1
2
3
定阶方法：
1.人为判断：自相关图显示出从第1阶之后的截尾性质，偏自相关图从第1阶之后显示出拖尾的性质，所以人为判断使用MA(1)模型，即ARMA(0,1,1)
2.相对最优模型识别，当p和q均小于等于3的所有组合的BIC信息量，取其中BIC信息量达到最小的模型阶数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#定阶
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
  tmp = []
  for q in range(qmax+1):
    try: #存在部分报错，所以用try来跳过报错。
      tmp.append(ARIMA(data, (p,1,q)).fit().bic)
    except:
      tmp.append(None)
  bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix) #从中可以找出最小值

p,q = bic_matrix.stack().idxmin() #先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%

pic7

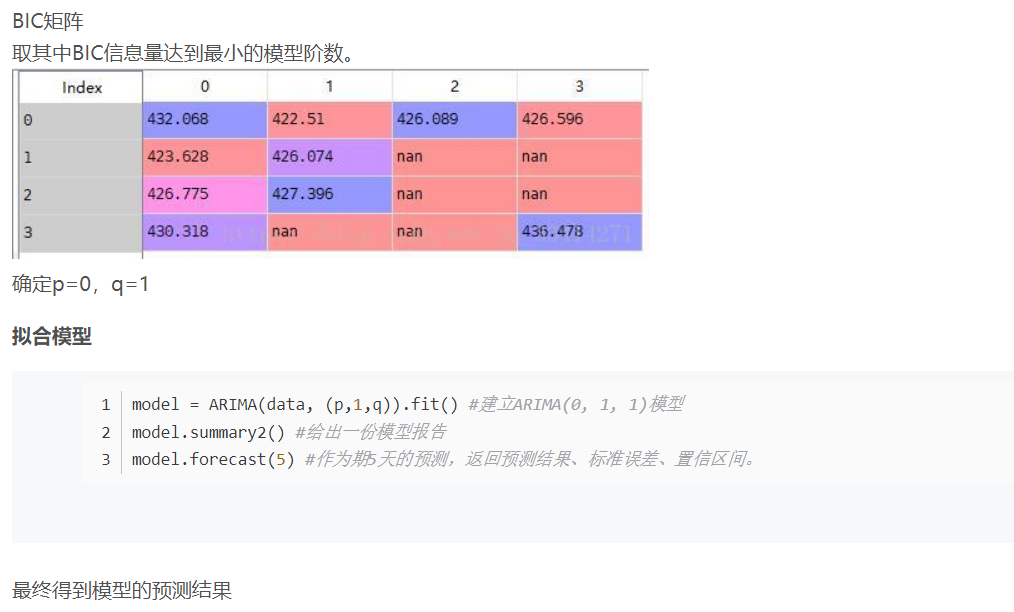
数据挖掘之时间序列分析

转自：https://blog.csdn.net/zjlamp/article/details/81606222

pic8

-------------本文结束感谢您的阅读-------------

Gitalking ...