最大熵
最大熵原理
最大熵原理是概率模型学习的一个准则:学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型
假设随机变量X的概率分布是P(X),则其熵为:
熵满足不等式,
|X|为x的取值个数,仅当X服从均匀分布时,熵最大
最大熵模型
应用最大熵原理得到的模型就是最大熵模型.
对于给定数据集,可以确定联合分布与边缘分布的经验分布公式,
用特征函数f(x,y)描述x,y之间的一个事件,定义为:
特征函数f(x,y)关于经验分布的期望为
特征函数关于模型与经验分布的期望为
该式可以作为模型学习的约束条件.假设有n个特征函数,则可以得到n个约束条件.
定义:在条件概率分布P(Y|X)上的条件熵H(P)最大的模型为最大熵模型
最大熵模型的学习
等价于如下的约束优化问题:
对于优化问题,下面采用拉格朗日乘子法.
省略计算过程.
得到:
另外由于P(y|x)关于y累加和为1,得到
Z称为规范化因子,f为特征函数,w为特征权值.所求的P即为最大熵模型.最后求解对偶问题外部的极大化问题
然后用极大似然估计来求解w.
理解最大熵
吴军博士在其所著的《数学之美》一书中曾经谈到:“有一次,我去AT&T实验室作关最大熵模型的报告,随身带了一个骰子。我问听众‘每个面朝上的概率分別是多少’,所有人都说是等概率,即各种点数的概率均为1/6。这种猜测当然是对的。我问听众为什么,得到的回答是一致的:对这个‘一无所知’的骰子,假定它毎一面朝上概率均等是最安全的做法。(你不应该主观假设它像韦小宝的骰子—样灌了铅。)从投资的角度看,就足风险最小的做法。从信息论的角度讲,就足保留了最大的不确定性,也就是说让熵达到最大。
接着我又告诉听众,我的这个骰子被我特殊处理过,已知四点朝上的概率是1/3,在这种情况下,每个面朝上的概率是多少?这次,大部分人认为除去四点的概率是1/3,其余的均是2/15,也就是说已知的条件(四点概率为1/3)必须满足,而对于其余各点的概率因为仍然无从知道,因此只好认为它们均等。注意,在猜测这两种不同情况下的概率分布时,大家都没有添加任何主观的假设,诸如四点的反面一定是三点等等。(事实上,有的骰子四点的反面不是三点而是一点。)这种基于直觉的猜测之所以准确,是因为它恰好符合了最大熵原理。”
我们可以对最大熵有一个基本的认识是:
“model all that is known and assume nothing about that which is unknown”
那么问题:什么是已知的?
我们的数据集就是已知的.
约束条件
通过数据集来确定约束条件.
假设分类模型是一个条件概率分布P(Y|X),X∈Input表示输入(特征向量),Y∈Output表示输出(分类标签).
特征函数
特征函数在这里其实就是相当于一个特征,用来描述输入x和y之间的某一事实(即x和y同时出现时给定一个特征值)
特征函数f(x,y)关于经验分布$\overline{P}(X,Y)$的期望值,用$E_{\overline{P}}(f)$表示.
而同理,$E_p(f)$表示f(x,y)在模型上关于实际联合分布P(X,Y)的数学期望,类似地则有
因此这里要求关于模型的联合分布P(X,Y)与经验分布$\overline{P}(X,Y)$的特征函数数学期望相等,说白了就是希望能让模型拟合数据集上的特征函数的数学期望
这里有个问题就是如何求P(x,y),可以有P(x,y)=P(x)P(y|x).但是P(x)是未知的.因此只能用$\overline{P}(X)$来近似.
则有
其中P(y|x)是模型。
逻辑回归与最大熵
我们从上面可以看到最大熵优化问题中求解P(y|x)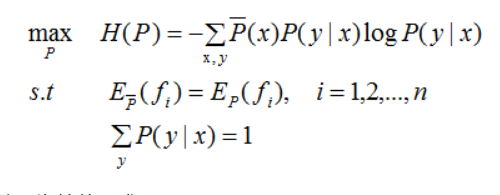
通过拉格朗日乘子法得到的是:
可以看到这里P(y|x)的形式与逻辑回归的softmax的形式类似.
softmax可以视为最大熵的P(y|x)的一种特例,即$f_i(x,y)=x_i$
注意:这里i=1,…,n表示的i是特征数.而约束就是对特征的约束.
总而言之,言而总之
逻辑回归先是直接假设数据的分布,二项分布或多项分布。
而最大熵是直接统计训练集中的各个特征与目标值的分布关系.(这就不需要我们猜测sigmoid或者softmax的函数形式)
一般模型中的说的特征都是指输入的特征,而最大熵模型中的”特征”指的是输入和输出有多么倾向于同时出现
可以以多类logistic regression为例,来感受一下两种视角的不同。
- 一般的视角下,每条输入数据会被表示成一个n维向量,可以看成n个特征。而模型中每一类都有n个权重,与n个特征相乘后求和再经过softmax的结果,代表这条输入数据被分到这个类的概率
- 在最大熵模型的视角下,每条输入的n个”特征”与k个类别共同组成了nk个特征,模型中有nk个权重,与特征一一对应.每个类别会触发nk个特征中的n个,这n个特征的加权和经过softmax,代表输入被分到各类的概率
